Egon and Ann Diczfalusy Foundation

Introduction

The idea of creation this software had been originated from many reviewers notes about used methods of randomization. They requested and missed the way how the groups were randomly filled-up with items and how the authors guaranteed the randomized selection? Luckily today’s informatics infrastructure provides great opportunities for generating real random numbers using industry accepted standards, like Microsoft RNGCryptoServiceProvider Class, which is the base of our solution, that was also accepted reviewing processes.

The aim of randomization studies in biomedicine is to be well-designed and conducted with high precision to assess the efficacy of treatments to ensure that each participant has an equal chance of receiving a particular treatment or not [1]. Random allocation of participants is based on probability theory, and approaching randomization in blocks or in strata provides a balancing of the subgroups with respect to features, which may affect the treatment prognosis. In principle, randomization could be performed in mechanical ways or by utilizing randomization programs or random number tables. Participants will be given a unique identifier and allocated to a trial group by an encoder before the study or at the time of the intervention when selecting particular outcomes of interest, which can be collected prospectively within a certain time-period. Nowadays, we mainly see random sequences produced by internet programs or randomization software in use. Internet services struggle to manage randomization and allocation processes and sometimes generate faulty sequences with specific/complex random allocation results. These services exhibit a limited potential to build a block random array and their output format is uncontrolled [2].

Randomization software has no restrictive abilities, and random allocation software was constructed for parallel group trials to avoid these flaws. However, we have found a weak point in this workflow: in creating groups, this software does not actually group subjects randomly to create trial groups [2], even though it provides much better results than online programs which use pseudo-randomization [3]. The importance of true randomization is considerable, and without it a study cannot really be treated as representative – as described in the “Statistics Guide for Research Grant Applicants” [4].

In the software available today, there are two ways to generate random numbers: true random numbers and pseudo- random numbers [5]. A true randomization process is superior in biomedical research because each number on the list is statistically independent of others. We developed a true random list generator through a repeat provision of the seed in pseudo-random processes using an algorithm, which, according to our knowledge, has not been published previously. We developed our own application using a modern programming environment: C#. The software requires a .NET runtime environment, so it works on any OS which implements .NET.

Technical background

Usually, software developers have to choose between (a) the swift but less reliable pseudo-random number generator (for example, Random Class) or (b) the true randomized values performed with a slower method (for example, RNGCryptoServiceProvider Class). Most computer programs are not free of charge and only generate pseudo-random sequences based on a mathematical formula. Pseudorandomization requires a shorter time-period due to low memory usage. Pseudo-random numbers are based on the computer’s internal clock; therefore, the “random” number can be predicted in a precisely defined time, as it is used in most applications. In most cases, the pseudo-random number list is so similar to the true random allocation set that it fulfills the requirements of randomization studies. In C#, pseudo-random numbers are chosen with equal probability from a finite set of numbers. Nevertheless, the numbers chosen are not completely random because the mathematical algorithm that is used to select them is predictable. Although the pseudo-random dataset is predetermined and sometimes periodically repeated, it is sufficiently random for practical purposes.

By contrast, true random generators use either various physical phenomena that are expected to be random or computational algorithms. The current implementation of Random Class is based on Donald E. Knuth’s subtractive random number generator algorithm [6]. A great deal of online and downloadable randomization software uses a simple Random Class program; for example, Cleanstat [7] and Minim [8] are MS-DOS-based software; Randomization.org [9] and Randomizer.org [10] are online services with limitations; and Random Allocation Software [11] and Research Randomizer [12] are 32-bit applications designed to run on Microsoft Windows 95 or later versions. Further sources can be found in the “Directory of randomization software and services” [13]. However, most of them have the limitations noted above, and, nowadays, most of the downloadable versions are not fully compatible with 64- bit versions of Windows.

Scientists usually analyse their data using complex applications like SPSS, R etc., with precision being a basic requirement in every step of the research workflow. Computers have become much faster recently. True number generation has therefore become available for a larger quantity of data: .NET “implements a cryptographic Random Number Generator (RNG) using the implementation provided by the Cryptographic Service Provider (CSP)” [14], which is called RNGCryptoServiceProvider Class.

Our implementation of real randomization

Our application has two methods to solve the problem of real randomization. The first one is the use of RNGCryptoServiceProvider Class, which generates true random numbers [15]. However, it has a strict limitation in .NET: it uses “byte” type numbers, which means it can contain a value of 0 to 255 in .NET [16]. In most cases, the number of subjects or groups could be fitted in this range, but an increasing number of studies comprise more subjects. The advantage of this solution is the rapid run, which is due to the fact that RNGCryptoServiceProvider Class is initialized only once in the application. Then the instance is called as many times as required according to a given parameter. On modern computers, this solution works quite fast, and its capacity could be sufficient for smaller studies with fewer than 255 subjects altogether.

The second method is the algorithm we have developed: the RPR algorithm (Reinitialized Pseudo Randomization algorithm). The RPR algorithm uses “16-bit integer” type numbers, so the maximum number it can handle is 32,767. This number of entries are considered to be large enough for biostatistical studies and advances, therefore a slower run is not a limitation [17].

RPR algorithm

The RPR algorithm [18] (Reinitialized Pseudo Randomization algorithm) was developed by Iván Devosa to provide a solution for true randomization and to handle large data in memory even for comprehensive studies (e.g. our studies on students at the University of Szeged, Hungary) [19]. The conceptualization of the algorithm relied upon the fact that. NET initializes Random Class, which uses the internal clock in the host computer. However, the list it generates comprises only pseudo-random numbers, and, hence, the pattern is predictable.

Nonetheless, if Random Class is reinitialized before every number generation in an algorithm, the numbers (except the first one) will be unpredictable because the time of the initiation is unknown. The time for every initialization depends on many factors in an everyday computer (hardware and software environment, current memory usage, current processor load, etc.), so the exact reinitialization times cannot be correctly predicted [20], a fact which can even be used against malicious attackers [21]. The difference between the predictions and real time will be greater in direct proportion to the number of values generated.

The implementation of the RPR algorithm in .NET (excerpt)

From the source code (Figure 1), it can be seen that the time of the next initialization depends on the execution time of the conditional code (and many other factors, noted above). The randomness is based on this “Achilles’ heel” in today’s personal computers.

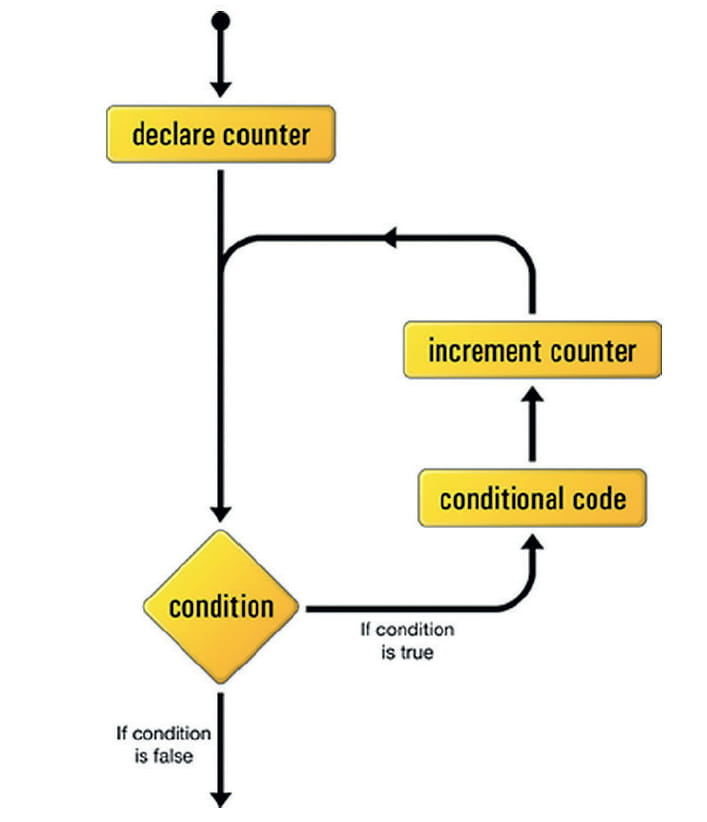
Using the application

We plan to use the graphical user interface (GUI) in multiple devices like classic “keyboard/mouse-based” PCs and Windows 8 touch screen devices. Please note: not all functions are available on every type of device and in every software environment.

• Step 1. The application is based on the .NET Runtime Environment. This environment is already preinstalled on computers using Windows 8, 8.1., 10, 11. This runtime environment is not installed on Windows 7, XP, 2000 or other operating systems, and we advise that you download the installer and description from the official Microsoft .NET website [23] (Figure 2).

• Step 2. The software does not call for conventional installation. It only requires the executable single file, and it is ready to run in a .NET Runtime Environment.
• Step 3. The language can be selected (Figure 3). The default languages for the software are English and Hungarian, and they are available with a single click.

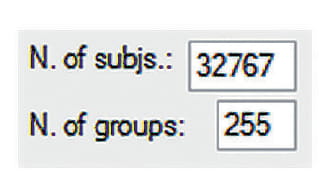
• Step 4. Two types of randomization are possible (Figure 4). The default randomization is RNGCryptoServiceProvider Class (if checkmark on) developed by Microsoft, with a maximum of 255 subjects or 255 groups. The advantage of this solution is the quick run on even slow computers. The other choice is the RPR algorithm (if checkmark off) we have developed (R4A program version 1.0), where the upper limit is 32,767 for subjects, which is the maximum 16-bit integer value, and 255 for groups. The advantage of this solution is the ability to work with a huge amount of data; however, the execution time can be quite long (even over 10 seconds), mostly on slower computers with little amount of memory.

• Step 5. The number of subjects and the number of groups required can be typed in (Figure 5). The application will automatically sort the randomly generated numbers into these groups.

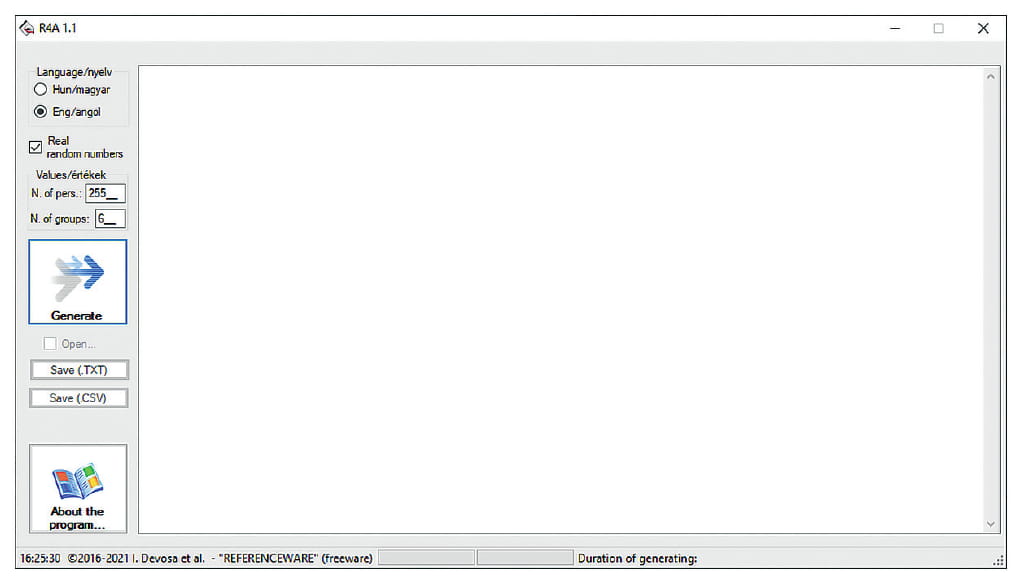
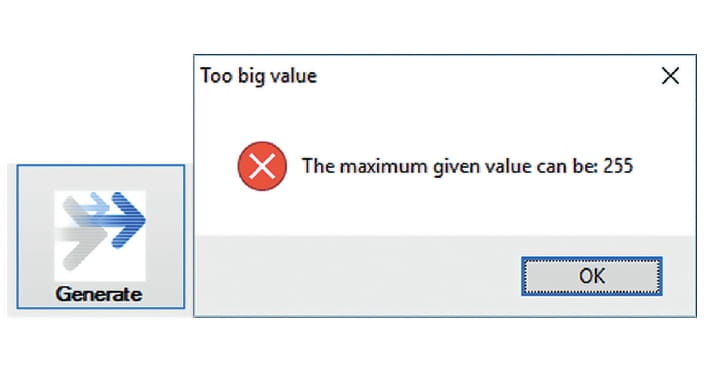
• Step 6. Click on the “GENERATE” button (Figure 6) to start the generation pre-process (Figure 7). If the range of available values is exceeded, an error message will be displayed.

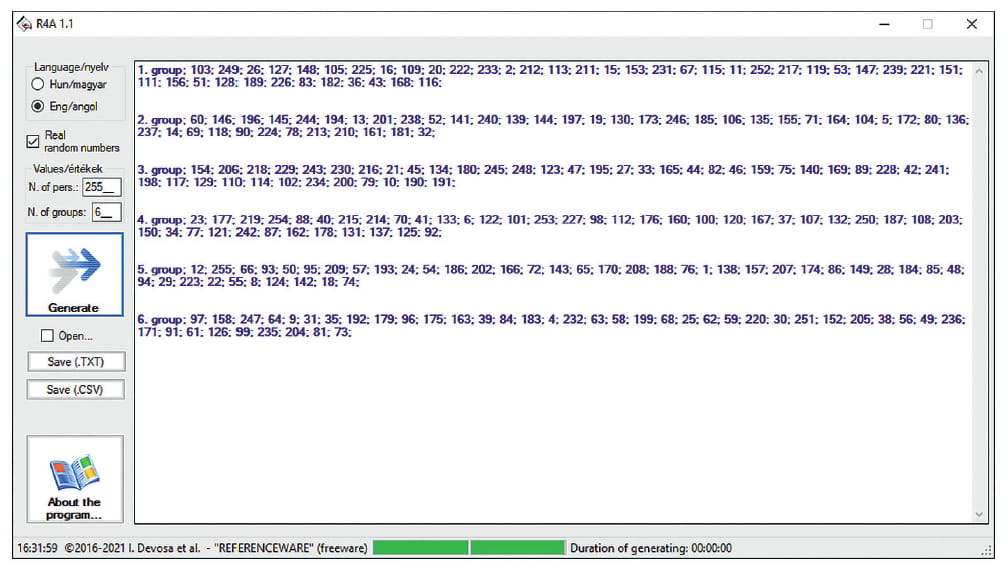
• Step 7. The generated real randomized numbers can be saved in two formats (Figure 8). The application will suggest “rav” (Random Allocated Values) as a filename, but this can be changed to any name. As a file type, choose ANSI text as an output for inserting the file into a document (e.g. an article in Word) or choose the CSV (comma separated values) format for database or statistical- analytical software.

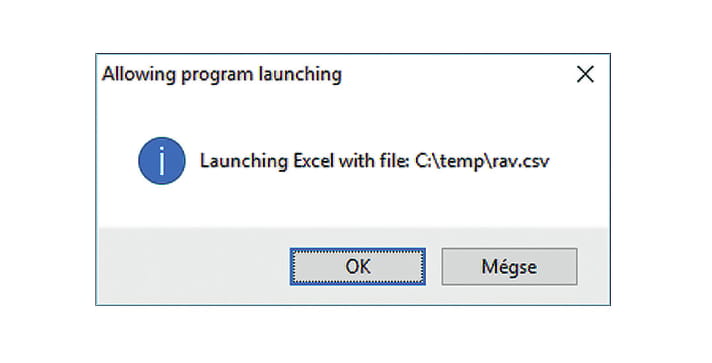
If “Open” is indicated, the application will automatically load the new values into Microsoft Excel (if had been installed before) and execute the program after saving, when you click on “Save (.CSV)” or does the same with Notepad, if you click on “Save (.TXT)”. Before execution, the application requests the user to allow running (Figure 9).

After execution, the data is ready for further use in Excel or other preinstalled software.

For detailed help or to see the reference to cite this article, click on the “About the program” button (Figure 10).

Discussion

We tested several pieces of randomization software, and none was suited to most of the computer environment (including .NET) and requirements (randomization independent of current time, working with a large number of subjects with output easily transferred to other software, etc.). There is a need for real randomization software that ensures that the items are statistically more independent of each other and that significantly decreases the hazard of a bias in the selection of study subjects. There is some real randomization software available, but it does not run properly in the .NET runtime environment.

We developed a program that would be a useful tool for simple randomization. In the application we developed, “R4A – Real Randomization for Representative Research Application 1.0”, we implemented two real randomizing solutions. The first solution is RNGCryptoServiceProvider Class developed by Microsoft, where it is possible to work with 255 values at most. The second one is our own RPR algorithm, with which we can theoretically generate as many random numbers as we need, but the computers’ RAM and CPU speed restrict our options. We therefore decided to use 16-bit integers with a maximum value of 32,767.

The R4A – 1.0 is based on the principles published in the “Introduction to Algorithm Analysis” [24], and it is a “referenceware” tool. It is permitted for use in scientific studies at no charge, but the current, updated descriptive article should be cited. The title of the latest version of the article can be found in APA (6th edition) format by clicking on the “About the program” button. The latest, free version is officialy available at authors’ website: http://devosa.hu/dll/r4a

Further efforts will be made as we develop the block randomization and minimization methods in the software, including support for multiple trials and address blinding.

References

All on-line sources were opened: 27.04.2021.

Download Full Article

• Ivan Devosa: R4A: “Real Randomization for Representative Research Application” 1.0 (2021, Journal of Hungarian Obstetricians and Gynaecologists, PDF, 5 pages, English, 2.0MB)